Introduction :
Cette méthode de compression est apparue vers la fin des années 80, on désirait a cet époque amélioré la rapidité d’échange des informations, un groupe d’experts du monde de la photographie a donc, en 1991, créer le format JPEG : Joint Photographic Expert Group.
La compression JPEG consiste à effectuer une dégradation de l’image indiscernable à l’œil, de façon à offrir un taux de compression beaucoup plus intéressant que les autres méthodes, donc à permettre de réduire considérablement l’espace occupé par le fichier sur le disque ou la vitesse de son transfert sur un réseau.
Pour ce faire, l’image est décomposée en blocs qui vont ensuite subir diverses opérations pour diminuer la taille de l’image initiale. Cette compression est donc une compression avec perte car elle subit une perte définitive d’information, même si il est possible de revenir à une image proche de l’image initiale avec certains procédés.
Voici le procédé de compression et de décompression JPEG d’une image :
Découpage en blocs de 8×8 pixels et transformation DCT :
Une image informatique est constituée de points de couleur uniforme : ce sont les pixels. Ils sont caractérisés par leur position dans l’image, et par leur couleur.
On peut représenter l’image par une matrice, qui a autant d’éléments que l’image a de pixels. Les coordonnées de ceux-ci sont données par leur position dans la matrice, et leur couleur par la valeur qu’ils ont dans la matrice.
On découpe ensuite cette matrice en sous matrice de 8×8 pixels.
A chacune de ces matrices on a applique ensuite la transformation DCT (Discrete Cosine Transform, ou Transformée en Cosinus Discrète). Cette technique est similaire de à la transformée de Fourier : transformation en somme de sinus et de cosinus de différentes fréquences et amplitude, mais pour la DCT on ne prend en compte que les cosinus.
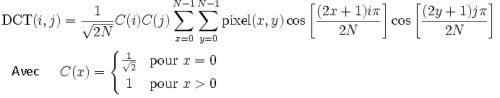
Chaque morceau d’image est donc représenté pas une somme de 64 fonctions cosinus de fréquence (hautes fréquences -> variation brusque de couleur entre 2 pixels, basses fréquences -> plage de couleur uniforme entre les pixels) et d’amplitude aux quels on associe une matrice ce qui nous donne une matrice tridimensionnelle 8×8x64
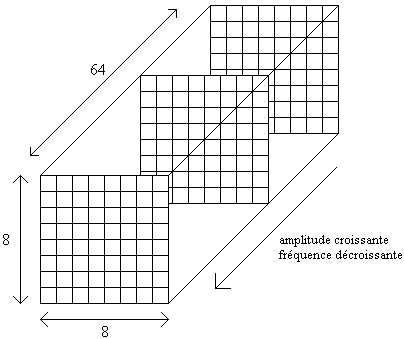
Prenons pour simplifier une matrice 8×8 qui est la somme des 64 matrices que compote un bloc.
Dans cette matrice est représenté les couleur de chaque pixel de l’image (chaque coordonnées correspond à une couleur d’un pixel)
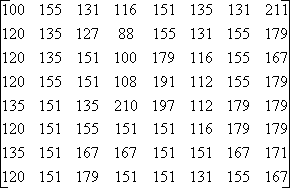
Matrice 1
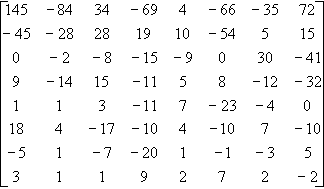
Matrice 2
La transformation de la matrice1 par la DCT donne la matrice2.
La transformation DCT est une transformation réversible, il n’y a donc pas de perte d’information à cette étape.
La quantification :
La quantification pondère l’importance des différents domaines de fréquences, sachant que la vision humaine est moins sensible aux hautes fréquences de détails. On va donc attribuer à chaque donnée un coefficient de poids qui correspond à son importance dans l’image. Cela revient à diviser les coefficients de Fourrier de l’image par ces coefficients de poids, et ne garder que ceux supérieurs à une certaine valeur.
Cela va nous permettre d’atténuer les hautes fréquences, c’est à dire celles auxquelles l’œil humain est très peu sensible. Ces fréquences ont des amplitudes faibles, et elles sont encore plus atténuées par la quantification (les coefficients sont même ramenés à 0).
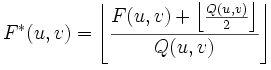
Q(i,j) = 1 + (1 + i + j) ´ Fq
avec Fq facteur de qualité et Q le pas de quantification.
Par exemple, pour Fq = 5 on obtient la matrice 3. On va finalement prendre la partie entière de la division de chaque valeur de la matrice 2 par la valeur de la matrice 3 ayant la même position, ce qui nous donne la matrice 4.
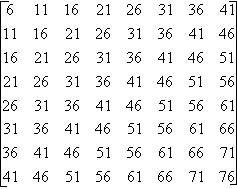

Matrice 3 Matrice 4
On peut remarquer que la matrice final (matrice 4) comporte un grand nombre de 0, c’est donc une valeur récurrente qui sera compressé pas un codage statique.
Codage statique :
On peut ici utiliser un code statique tel que le codage de Huffman.
Exemple du déroulement de la compression d’un bloc d’une image
La compression avec pertes, aussi appelée compression irréversible ou non conservative, est utilisée pour les médias qui font appel à nos sens.
Elle consiste à accepter une dégradation du média décompressé. Cette dégradation devra être indiscernable ou suffisamment réduite pour ne pas être perçue par nos sens et ne pas altérer la compréhension générale du média.
La compression de données avec pertes est donc utilisée lors de la compression d’images, de musiques ou encore de vidéos.
En effet pour ces types de médias, une dégradation lors de la décompression n’est pas forcément un problème. Prenons l’exemple de la musique : une oreille normale ne fait pas systématiquement la distinction entre une musique provenant d’un CD audio ou d’un fichier au format de compression mp3.
Pourtant le débit binaire est complètement différent : un CD audio a un débit de 176.4 Ko/s soit 1,4 Mbit/s alors que le mp3 a un débit de 192 Kbit/s (en général), et pourtant la différence est souvent indiscernable pour la plupart des personnes. Et si l’oreille ne fait pas de différence, il n’est donc pas nécessaire d’utiliser un format non compressé qui prend de la place et qui est de “même” qualité (pour nous utilisateur) qu’un format compressé.
La compression avec pertes, qui est donc un procédé irréversible (i.e. il n’y a pas de retour en arrière possible), est basée sur la perception des images et du son par nos oreilles et nos yeux. On va donc jouer sur cette perception pour compresser le fichier.
Par exemple, pour une image, on va regrouper les pixels de même couleur en zones, ou dans une vidéo, on va garder pour une séquence seulement les parties de l’image qui changent par rapport à l’image précédente et supprimer la partie redondante.
