En 1952, David Albert Huffman, alors étudiant au MIT (Massachusetts Institute of Technology), mit au point le codage qui porte son nom : le codage de Huffman (Huffman coding en anglais). Il publia cette même année “A Method for the Construction of Minimum-Redundancy Codes” (ici au format pdf), où il explique sa méthode.

Une source d’informations est définie par un alphabet (ensemble de symboles) et par une distribution de probabilités définissant la probabilité d’apparition de chaque symbole. Le codage de Huffman est une méthode de compression statistique, faisant donc intervenir la distribution de probabilités de la source. Il s’agit d’un codage entropique :  l’entropie étant la quantité moyenne d’informations par symbole (formule), elle est exprimée en bits/symbole. Elle est maximale pour une source lorsque tous les symboles sont équiprobables. Moins une source est redondante plus elle porte d’informations et donc plus son entropie est élevée.

La méthode de Huffman utilise un code à longueur variable pour chaque symbole. Ainsi, un symbole revenant souvent sera codé sur un nombre de bits moins important qu’un symbole n’apparaissant que rarement. Le taux de compression est limité par une limite théorique : l’entropie. On peut noter que si les symboles étaient équiprobables, un code à longueur fixe pour coder chaque symbole serait optimal et l’entropie donnerait la longueur minimale de ce code fixe.

Le principe de cette méthode repose sur la construction d’un arbre de codage. Prenons un exemple afin de comprendre sa construction. Cet exemple est tiré du cours de “Transmission” de Thomas SPRÖSSER donné en première année dans notre école.

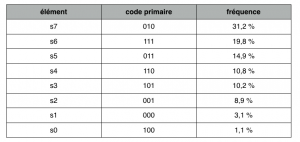
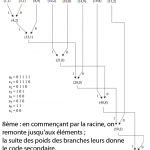
Nous prendrons un vocabulaire de 8 éléments (s0, s1 … s7). Tout d’abord, dressons un tableau faisant apparaître le codage primaire (de longueur fixe) de chaque élément dans l’ordre décroissant de la fréquence d’apparition de ces derniers :

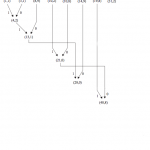
Étapes de la construction de l’arbre :

1ère étape : on écrit les symboles du code primaire dans l’ordre croissant.

2ème étape : on regroupe les deux premiers éléments du code (i.e. les deux revenants le moins souvent) en additionnant leur fréquence.

3ème étape : avec ces deux éléments comme des branches, on créé un nœud en associant la valeur 0 aux
branches droites et la valeur 1 aux branches gauches.

4ème étape : on donne au nœud créé la somme des fréquences de ces deux fils.

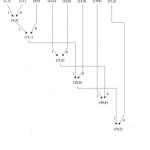
5ème étape : on sélectionne, parmi tous les éléments et nœuds les deux dont la fréquence est la plus faible.

6ème étape : on répète le schéma de création d’un nouveau nœud et on lui attribue sa fréquence.

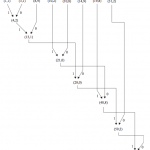
7ème étape : on continue jusqu’à obtenir la racine de l’arbre.

8ème et dernière étape : en commençant par la racine, on remonte jusqu’aux éléments ; la suite des poids des branches leur donne le code secondaire.

Visualisez toutes ces étapes en image (vous pouvez utiliser les boutons PREV/NEXT au bord des imges, après avoir cliqué sur la première image)

L’algorithme de Huffman est encore très utilisé de nos jours. La norme non conservative JPEG, après avoir éliminé un certain type d’informations, compresse les données restantes à l’aide de cet algorithme. Il est également utilisé pour la transmission de fax, mais également par la plupart des compresseurs comme second étage de compression (i.e. qu’après avoir été comprimé par une autre technique, les données sont surcomprimées à l’aide de l’algorithme de Huffman) .

Il existe différents procédés pour compresser une information sans pertes, nous allons dans cet exemple nous intéresser à l’une des plus simples d’entre elles : le Run Length Encoding (RLE) (codage par plages en français).
Cet algorithme de compression est du point de vue théorique très simple à appréhender. En effet, on ne fait que remplacer des éléments identiques se succédant par un seul de ces éléments, suivi du nombre de répétitions.

exemple :

• donnée source : Moogli
• donnée compressée : M$2ogli

On peut voir avec cet exemple que la donnée compressée prend plus de place que la donnée source (7 caractères contre 6). Il est donc important de fixer un seuil du nombre de répétitions minimales à partir duquel on codera cette répétition afin d’éviter ce genre de situation, le but de la compression étant bien entendu de gagner de la place.
Le caractère ‘$’ est ici choisi comme caractère spécial (arbitraire), il permet d’indiquer une compression, et il est essentiel pour la phase de décompression (i.e. pour pouvoir retrouver la donnée source à partir de la donnée compressée).
On montre pour ces raisons que le seuil doit être supérieur ou égal à 4.

Ainsi, en appliquant un seuil  de 4 on aura :

• donnée source : Moogli
• donnée compressée : Moogli

dans ce cas on ne gagne aucune place mais en tout cas on n’en perd plus.

Prenons un autre exemple :

• donnée source : Heeeellooooo
• donnée compressée : H$4ell$5o

on obtient une compression de 25% (on gagne 3 caractères sur 12).

Cette méthode n’offre malheureusement que de médiocres résultats. Par le passé, elle a été beaucoup utilisée, essentiellement pour la compression d’images. Il est en effet plus aisé de trouver des répétitions successives d’un pixel de même couleur dans une image qu’une répétition successive d’une lettre dans un texte en langue française par exemple. Dans le cas d’une image matricielle (bitmap en anglais) l’information est stockée sous la forme d’un tableau de points de couleurs (pixels). Dans une zone de l’image où la couleur est homogène on pourra donc trouver des successions de pixels identiques, et ainsi gagner en place de stockage à l’aide d’une méthode de compression tel que le RLE.

La compression sans perte (lossless data compression en anglais), appelée aussi compactage consiste en une nouvelle représentation d’une information sous une forme plus condensée.  Le fait que l’on garde exactement la même quantité d’information avant et après la compression en fait une opération réversible.

Pour des données telles que du texte, un programme exécutable, un tableau excel, etc., une compression sans perte est indispensable, on ne peut pas se permettre d’altérer l’information originale.

La compression sans perte se base sur le fait que la plupart des données possèdent une certaine redondance statistique. Prenons un exemple simple : un texte écrit en langue française, statistiquement on y trouvera plus de e, s ou encore de a que de x ou y (source). Dans l’article précédent on pouvait compter ainsi 97 e, 78 r pour seulement 2 y ou un seul k. Il y a également peu de chance qu’un k suive un z. On pourra ainsi gagner de la place lors du codage d’une information en se basant sur la fréquence d’apparition des caractères dans le cas d’un texte.

Nous verrons dans le prochain article un exemple de mise en pratique de ce type de compression.