Introduction :
Cette méthode de compression est apparue vers la fin des années 80, on désirait a cet époque amélioré la rapidité d’échange des informations, un groupe d’experts du monde de la photographie a donc, en 1991, créer le format JPEG : Joint Photographic Expert Group.
La compression JPEG consiste à effectuer une dégradation de l’image indiscernable à l’œil, de façon à offrir un taux de compression beaucoup plus intéressant que les autres méthodes, donc à permettre de réduire considérablement l’espace occupé par le fichier sur le disque ou la vitesse de son transfert sur un réseau.
Pour ce faire, l’image est décomposée en blocs qui vont ensuite subir diverses opérations pour diminuer la taille de l’image initiale. Cette compression est donc une compression avec perte car elle subit une perte définitive d’information, même si il est possible de revenir à une image proche de l’image initiale avec certains procédés.
Voici le procédé de compression et de décompression JPEG d’une image :
Découpage en blocs de 8×8 pixels et transformation DCT :
Une image informatique est constituée de points de couleur uniforme : ce sont les pixels. Ils sont caractérisés par leur position dans l’image, et par leur couleur.
On peut représenter l’image par une matrice, qui a autant d’éléments que l’image a de pixels. Les coordonnées de ceux-ci sont données par leur position dans la matrice, et leur couleur par la valeur qu’ils ont dans la matrice.
On découpe ensuite cette matrice en sous matrice de 8×8 pixels.
A chacune de ces matrices on a applique ensuite la transformation DCT (Discrete Cosine Transform, ou Transformée en Cosinus Discrète). Cette technique est similaire de à la transformée de Fourier : transformation en somme de sinus et de cosinus de différentes fréquences et amplitude, mais pour la DCT on ne prend en compte que les cosinus.
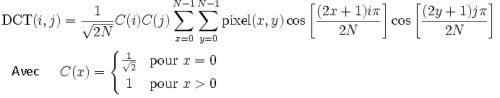
Chaque morceau d’image est donc représenté pas une somme de 64 fonctions cosinus de fréquence (hautes fréquences -> variation brusque de couleur entre 2 pixels, basses fréquences -> plage de couleur uniforme entre les pixels) et d’amplitude aux quels on associe une matrice ce qui nous donne une matrice tridimensionnelle 8×8x64
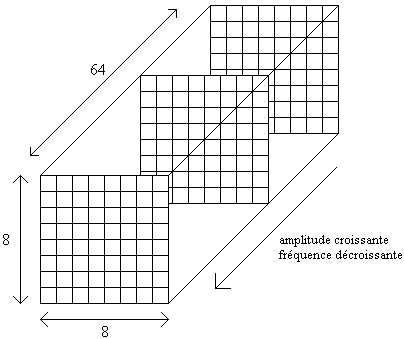
Prenons pour simplifier une matrice 8×8 qui est la somme des 64 matrices que compote un bloc.
Dans cette matrice est représenté les couleur de chaque pixel de l’image (chaque coordonnées correspond à une couleur d’un pixel)
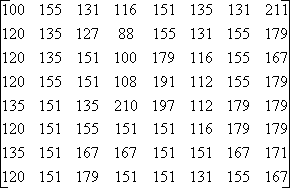
Matrice 1
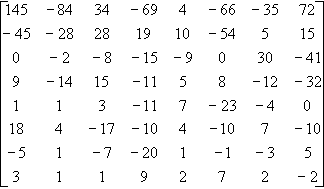
Matrice 2
La transformation de la matrice1 par la DCT donne la matrice2.
La transformation DCT est une transformation réversible, il n’y a donc pas de perte d’information à cette étape.
La quantification :
La quantification pondère l’importance des différents domaines de fréquences, sachant que la vision humaine est moins sensible aux hautes fréquences de détails. On va donc attribuer à chaque donnée un coefficient de poids qui correspond à son importance dans l’image. Cela revient à diviser les coefficients de Fourrier de l’image par ces coefficients de poids, et ne garder que ceux supérieurs à une certaine valeur.
Cela va nous permettre d’atténuer les hautes fréquences, c’est à dire celles auxquelles l’œil humain est très peu sensible. Ces fréquences ont des amplitudes faibles, et elles sont encore plus atténuées par la quantification (les coefficients sont même ramenés à 0).
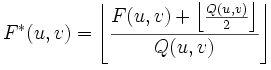
Q(i,j) = 1 + (1 + i + j) ´ Fq
avec Fq facteur de qualité et Q le pas de quantification.
Par exemple, pour Fq = 5 on obtient la matrice 3. On va finalement prendre la partie entière de la division de chaque valeur de la matrice 2 par la valeur de la matrice 3 ayant la même position, ce qui nous donne la matrice 4.
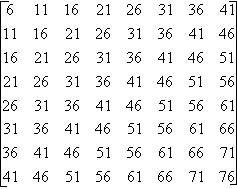

Matrice 3 Matrice 4
On peut remarquer que la matrice final (matrice 4) comporte un grand nombre de 0, c’est donc une valeur récurrente qui sera compressé pas un codage statique.
Codage statique :
On peut ici utiliser un code statique tel que le codage de Huffman.
Exemple du déroulement de la compression d’un bloc d’une image
Voyons maintenant comment compresser des fichiers si vous êtes utilisateur de Mac Os X.
Nous allons commencer par un logiciel gratuit (7zX).
C’est un utilitaire d’archivage qui supporte en lecture les fichiers de type : tar, zip, gzip, bzip2, UNIX compress, 7z et s7z. En écriture, il utilise l’algorithme LZMA au format 7z, qui est malheureusement le seul format possible pour la création d’archive, mais qui d’un autre coté est très performant en terme de compression. A noté également que le format rar n’est pas supporté en lecture.
De sont coté, son utilisation est très simple, en effet, pour ouvrir une archive il suffira de glissé/déposé celle ci sur l’icône de l’application.
Pour ce qui est de la création d’une archive, même système : glissé un fichier ou un dossier sur l’icône de l’application. Ensuite, une fenêtre s’ouvre, vous proposant quelques options parmi les plus courantes.
Les différentes options détaillées :
- Vous pouvez définir le niveau de compression : de Store à Ultra.
- En cochant la case Preserve Macintosh resource forks afin de conserver votre fichier original.
- Vous pourrez activer la création d’une archive auto-extractible
- Vous pouvez entrer un mot de passe pour crypter vos archives avec l’algorithme AES -256.
- Enfin, si vous désirez créer une archive partitionnée, vous pouvez définir la taille de volume désiré.
Si vous souhaitez compresser au format zip sachez que Tiger (Mac OS 10.4) et Leopard (Mac OS 10.5) possède un archiveur zip. Pour cela, clic droit sur un dossier ou un fichier puis Compresser “le nom du fichier ou dossier”. Voir ci dessous :
Pour ce qui est du format rar, il existe UnRarX, qui est également assez simple d’utilisation et qui est gratuit.
Vous choisissez à partir de “Extract to” l’endroit où vous souhaitez désarchiver l’archive rar :
- File directory : l’archive sera décompressée dans le dossier où se trouve l’archive en question
- Desktop : l’archive sera décompressée sur le bureau
- Other : l’archive sera décompressée dans le dossier de votre choix
Ensuite, il ne reste plus pour vous qu’à glisser/déposer l’archive que vous souhaitez décompresser dans la fenêtre de l’application.
Ce tutoriel est destiné aux débutants en informatique et explique comment compresser des fichiers avec trois logiciels différents.
Compresser des fichiers peut être utile pour gagner de la place sur son disque dur, pour envoyer des fichiers par email en un seul bloc, pour découper un fichier trop gros en plusieurs fichiers de taille plus petite (par exemple pour graver des données sur plusieurs CD…)
On va commencer par voir la compression de fichiers sous Windows XP et Windows Vista :
Pour ce faire, il suffit simplement de sélectionner les fichiers ou les dossiers que vous voulez compresser, ensuite vous faites un clic droit sur l’un des fichiers sélectionnés, allez sur “Envoyer vers” puis “Dossier compressé”.
Cela vous crée un fichier avec une extension .zip dans le dossier courant qui portera le nom du fichier sur lequel vous avez fait le clic droit.
La compression de fichier avec 7-Zip :
7-Zip est un logiciel gratuit et très complet. Il permet de compresser des fichiers avec différents taux de compression, de découper des fichiers en plusieurs archives et même de crypter les archives. Il propose aussi un choix dans le format de l’archive (i.e. l’algorithme de compression utilisé).
Comme pour la compression avec Windows, vous sélectionnez les fichiers et/ou dossiers que vous souhaitez compresser, clic droit sur un des fichiers sélectionnés, allez sur “7-Zip” puis sur “Ajouter à l’archive…”.
Cela vous ouvre une fenêtre qui vous propose plusieurs options.
Ecrivez en (1) le nom que vous voulez donner à votre archive et en (2) choisissez l’emplacement où elle va être créée.
En (3), vous pouvez choisir le format de votre archive.
En (4), vous pouvez sélectionner le taux de compression que vous voulez attribuer à votre archive.
Entrez en (5) la taille de partitionnement de votre archive, si vous voulez la partitionner (i.e. découper l’archive en plusieurs archives), sinon laissez vide.
Dans le cadre (6), vous pouvez crypter votre archive avec un mot de passe.
Enfin, créer votre archive en cliquant sur “Ok”.
La compression avec WinRar :
WinRar est un logiciel payant, également très complet et qui permet de faire les même choses que 7-Zip. Alors pourquoi présenter ce logiciel? Car il est très répandu et il est donc intéressant de savoir comment créer une archive avec.
Comme pour les précédents, vous sélectionnez les fichiers et/ou dossiers que vous voulez archiver, vous faites un clic droit sur l’un des fichiers sélectionnés puis vous sélectionnez “Ajouter à l’archive…”.
Cela vous ouvre une fenêtre qui propose plusieurs options.
Les options proposées sont à peu près les mêmes que pour 7-Zip. On retrouve le choix du nom de l’archive, son emplacement de création, le choix du format de l’archive, le taux de compression, la taille de partitionnement et le cryptage de l’archive (placé ici dans l’onglet “Avancé” puis en cliquant sur “Mot de passe…”).
La compression avec pertes, aussi appelée compression irréversible ou non conservative, est utilisée pour les médias qui font appel à nos sens.
Elle consiste à accepter une dégradation du média décompressé. Cette dégradation devra être indiscernable ou suffisamment réduite pour ne pas être perçue par nos sens et ne pas altérer la compréhension générale du média.
La compression de données avec pertes est donc utilisée lors de la compression d’images, de musiques ou encore de vidéos.
En effet pour ces types de médias, une dégradation lors de la décompression n’est pas forcément un problème. Prenons l’exemple de la musique : une oreille normale ne fait pas systématiquement la distinction entre une musique provenant d’un CD audio ou d’un fichier au format de compression mp3.
Pourtant le débit binaire est complètement différent : un CD audio a un débit de 176.4 Ko/s soit 1,4 Mbit/s alors que le mp3 a un débit de 192 Kbit/s (en général), et pourtant la différence est souvent indiscernable pour la plupart des personnes. Et si l’oreille ne fait pas de différence, il n’est donc pas nécessaire d’utiliser un format non compressé qui prend de la place et qui est de “même” qualité (pour nous utilisateur) qu’un format compressé.
La compression avec pertes, qui est donc un procédé irréversible (i.e. il n’y a pas de retour en arrière possible), est basée sur la perception des images et du son par nos oreilles et nos yeux. On va donc jouer sur cette perception pour compresser le fichier.
Par exemple, pour une image, on va regrouper les pixels de même couleur en zones, ou dans une vidéo, on va garder pour une séquence seulement les parties de l’image qui changent par rapport à l’image précédente et supprimer la partie redondante.
En 1952, David Albert Huffman, alors étudiant au MIT (Massachusetts Institute of Technology), mit au point le codage qui porte son nom : le codage de Huffman (Huffman coding en anglais). Il publia cette même année “A Method for the Construction of Minimum-Redundancy Codes” (ici au format pdf), où il explique sa méthode.
Une source d’informations est définie par un alphabet (ensemble de symboles) et par une distribution de probabilités définissant la probabilité d’apparition de chaque symbole. Le codage de Huffman est une méthode de compression statistique, faisant donc intervenir la distribution de probabilités de la source. Il s’agit d’un codage entropique : l’entropie étant la quantité moyenne d’informations par symbole (formule), elle est exprimée en bits/symbole. Elle est maximale pour une source lorsque tous les symboles sont équiprobables. Moins une source est redondante plus elle porte d’informations et donc plus son entropie est élevée.
La méthode de Huffman utilise un code à longueur variable pour chaque symbole. Ainsi, un symbole revenant souvent sera codé sur un nombre de bits moins important qu’un symbole n’apparaissant que rarement. Le taux de compression est limité par une limite théorique : l’entropie. On peut noter que si les symboles étaient équiprobables, un code à longueur fixe pour coder chaque symbole serait optimal et l’entropie donnerait la longueur minimale de ce code fixe.
Le principe de cette méthode repose sur la construction d’un arbre de codage. Prenons un exemple afin de comprendre sa construction. Cet exemple est tiré du cours de “Transmission” de Thomas SPRÖSSER donné en première année dans notre école.
Nous prendrons un vocabulaire de 8 éléments (s0, s1 … s7). Tout d’abord, dressons un tableau faisant apparaître le codage primaire (de longueur fixe) de chaque élément dans l’ordre décroissant de la fréquence d’apparition de ces derniers :
Étapes de la construction de l’arbre :
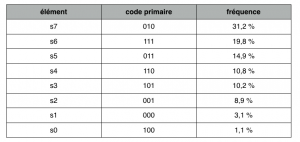
1ère étape : on écrit les symboles du code primaire dans l’ordre croissant.
2ème étape : on regroupe les deux premiers éléments du code (i.e. les deux revenants le moins souvent) en additionnant leur fréquence.
3ème étape : avec ces deux éléments comme des branches, on créé un nœud en associant la valeur 0 aux
branches droites et la valeur 1 aux branches gauches.
4ème étape : on donne au nœud créé la somme des fréquences de ces deux fils.
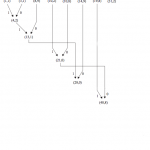
5ème étape : on sélectionne, parmi tous les éléments et nœuds les deux dont la fréquence est la plus faible.
6ème étape : on répète le schéma de création d’un nouveau nœud et on lui attribue sa fréquence.
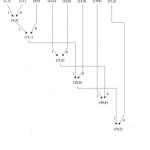
7ème étape : on continue jusqu’à obtenir la racine de l’arbre.
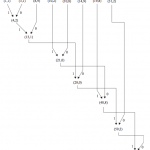
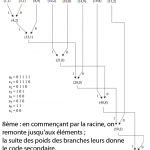
8ème et dernière étape : en commençant par la racine, on remonte jusqu’aux éléments ; la suite des poids des branches leur donne le code secondaire.
Visualisez toutes ces étapes en image (vous pouvez utiliser les boutons PREV/NEXT au bord des imges, après avoir cliqué sur la première image)
L’algorithme de Huffman est encore très utilisé de nos jours. La norme non conservative JPEG, après avoir éliminé un certain type d’informations, compresse les données restantes à l’aide de cet algorithme. Il est également utilisé pour la transmission de fax, mais également par la plupart des compresseurs comme second étage de compression (i.e. qu’après avoir été comprimé par une autre technique, les données sont surcomprimées à l’aide de l’algorithme de Huffman) .